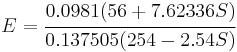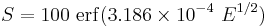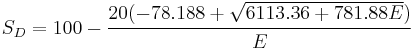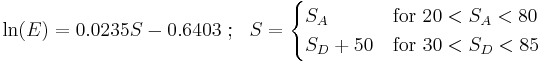Shore durometer
Durometer is one of several measures of the hardness of a material. Hardness may be defined as a material's resistance to permanent indentation. The durometer scale was defined by Albert F. Shore, who developed a measurement device called a durometer in the 1920s. The term durometer is often used to refer to the measurement, as well as the instrument itself. Durometer is typically used as a measure of hardness in polymers, elastomers, and rubbers.[1]
Contents |
Durometer scales
There are several scales of durometer, used for materials with different properties. The two most common scales, using slightly different measurement systems, are the ASTM D2240 type A and type D scales. The A scale is for softer plastics, while the D scale is for harder ones. However, the ASTM D2240-00 testing standard calls for a total of 12 scales, depending on the intended use; types A, B, C, D, DO, E, M, O, OO, OOO, OOO-S, and R. Each scale results in a value between 0 and 100, with higher values indicating a harder material.[2]
Method of measurement
Durometer, like many other hardness tests, measures the depth of an indentation in the material created by a given force on a standardized presser foot. This depth is dependent on the hardness of the material, its viscoelastic properties, the shape of the presser foot, and the duration of the test. ASTM D2240 durometers allows for a measurement of the initial hardness, or the indentation hardness after a given period of time. The basic test requires applying the force in a consistent manner, without shock, and measuring the hardness (depth of the indentation). If a timed hardness is desired, force is applied for the required time and then read. The material under test should be a minimum of 6.4 mm (.25 inch) thick.[3]
| Durometer | Indenting foot | Applied mass [kg] | Resulting force [N] |
|---|---|---|---|
| Type A | Hardened steel rod 1.1 mm - 1.4 mm diameter, with a truncated 35° cone, 0.79 mm diameter | 0.822 | 8.064 |
| Type D | Hardened steel rod 1.1 mm - 1.4 mm diameter, with a 30° conical point, 0.1 mm radius tip | 4.550 | 44.64 |
The ASTM D2240 standard recognizes twelve different durometer scales using combinations of specific spring forces and indentor configurations. These scales are properly referred to as durometer types; i.e. a durometer type is specifically designed to determine a specific scale, and the scale does not exist separately from the durometer. The table below provides details for each of these types, with the exception of Type R.[4]
| Durometer Type | Configuration | Diameter | Extension | Spring force |
|---|---|---|---|---|
| A | 35° truncated (frustum) cone | 1.40 mm (0.055 in) | 2.54 mm (0.100 in) | 822 gf (8.06 N) |
| C | 35° truncated (frustum) cone | 1.40 mm (0.055 in) | 2.54 mm (0.100 in) | 4,536 gf (44.48 N) |
| D | 30° cone | 1.40 mm (0.055 in) | 2.54 mm (0.100 in) | 4,536 gf (44.48 N) |
| B | 30° cone | 1.40 mm (0.055 in) | 2.54 mm (0.100 in) | 822 gf (8.06 N) |
| M | 30° cone | 0.79 mm (0.031 in) | 1.25 mm (0.049 in) | 78 gf (0.76 N) |
| E | 2.5 mm (0.098 in) spherical radius | 4.50 mm (0.177 in) | 2.54 mm (0.100 in) | 822 gf (8.06 N) |
| O | 1.20 mm (0.047 in) spherical radius | 2.40 mm (0.094 in) | 2.54 mm (0.100 in) | 822 gf (8.06 N) |
| OO | 1.20 mm (0.047 in) spherical radius | 2.40 mm (0.094 in) | 2.54 mm (0.100 in) | 113 gf (1.11 N) |
| DO | 1.20 mm (0.047 in) spherical radius | 2.40 mm (0.094 in) | 2.54 mm (0.100 in) | 4,536 gf (44.48 N) |
| OOO | 0.635 mm (0.0250 in) spherical radius | 10.7 mm (0.42 in) - 11.6 mm (0.46 in) | 2.54 mm (0.100 in) | 113 gf (1.11 N) |
| OOO-S | 10.7 mm (0.42 in) radius disk | 12.0 mm (0.47 in) | 5.0 mm (0.20 in) | 197 gf (1.93 N) |
Note: "Type R is a designation, rather than a true ‘type’. The R designation specifies a presser foot diameter (hence the R, for radius, obviously D could not be used) of 18 ± 0.5 mm (0.71 ± 0.02 in) in diameter, while the spring forces and indentor configurations remain unchanged. The R designation is applicable to any D2240 Type, with the exception of Type M; the R designation is expressed as Type xR, where x is the D2240 type, e.g. aR, dR, etc.; the R designation also mandates the employment of an operating stand".[4]
The final value of the hardness depends on the depth of the indenter after it has been applied for 15sec on the material. If the indenter penetrates 2.54 mm (0.100 inch) or more into the material, the durometer is 0 for that scale. If it does not penetrate at all, then the durometer is 100 for that scale. It is for this reason that multiple scales exist. Durometer is a dimensionless quantity, and there is no simple relationship between a material's durometer in one scale, and its durometer in any other scale, or by any other hardness test.[1]
| Material | Durometer | Scale |
|---|---|---|
| Bicycle gel seat | 15-30 | OO |
| Chewing gum | 20 | OO |
| Sorbothane | 40 | OO |
| Sorbothane | 30-70 | A |
| Rubber band | 25 | A |
| Door seal | 55 | A |
| Automotive tire tread | 70 | A |
| Soft wheels of rollerskates and skateboard | 78 | A |
| Hydraulic O-ring | 70-90 | A |
| Hard wheels of rollerskates and skateboard | 98 | A |
| Ebonite Rubber | 100 | A |
| Solid truck tires | 50 | D |
| Hard hat (typically HDPE) | 75 | D |
Relation between Shore hardness and elastic modulus
A semi-empirical relation between the Shore hardness and the Young's modulus for elastomers has been derived by Gent.[5] This relation has the form
where  is the Young's modulus in MPa and
is the Young's modulus in MPa and  is the Shore hardness. This relation gives a value of
is the Shore hardness. This relation gives a value of 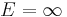 at
at 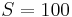 but departs from experimental data for
but departs from experimental data for 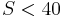 .
.
Another relation that fits the experimental data slightly better is[6]
where 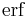 is the error function and
is the error function and  is in units of Pa.
is in units of Pa.
A first order estimate of the relation between Shore D hardness and the elastic modulus for a conical indenter with a 15 degree cone is [7]
where 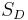 is the Shore-D hardness and
is the Shore-D hardness and  is in MPa.
is in MPa.
Another linear relation between the Shore hardness and the natural logarithm of Young's modulus is applicable over a large range of Shore A and Shore D hardnesses.[7] This relation has the form:
where 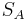 is the Shore A hardness,
is the Shore A hardness,  is the Shore D hardness, and
is the Shore D hardness, and  is the Young's modulus in MPa.
is the Young's modulus in MPa.
Patents
- US patent 1770045, A.F. Shore, "Apparatus for Measuring the Hardness of Materials", issued 1930-07-08
- US patent 2421449, J.G. Zuber, "Hardness Measuring Instrument", issued 1947-06-03
See also
- Brinell hardness test
- Bloom (test)
- Hardness
- Knoop hardness test
- Leeb Rebound Hardness Test
- Rockwell hardness test
- Vickers hardness test
References
- ^ a b "Shore (Durometer) Hardness Testing of Plastics". http://www.matweb.com/reference/shore-hardness.asp. Retrieved 2006-07-22.
- ^ "Material Hardness". CALCE and the University of Maryland. 2001. http://www.calce.umd.edu/general/Facilities/Hardness_ad_.htm#3.5. Retrieved 2006-07-22.
- ^ a b "Rubber Hardness". National Physical Laboratory, UK. 2006. http://www.npl.co.uk/server.php?show=ConWebDoc.379. Retrieved 2006-07-22.
- ^ a b "DuroMatters! Basic Durometer Testing Information". CCSi, Inc.. http://www.ccsi-inc.com/t-durometer-testing.pdf. Retrieved 29 May 2011.
- ^ A.N. Gent, (1958), On the relation between indentation hardness and Young's modulus, Institution of Rubber Industry -- Transactions, 34, pp. 46–57.
- ^ British Standard 903, (1950,1957), Methods of testing vulcanised rubber Part 19 (1950) and Part A7 (1957).
- ^ a b Qi, HJ and Joyce, K. and Boyce, MC, (2003), Durometer hardness and the stress-strain behavior of elastomeric materials, Rubber Chemistry and Technology, 76(2), pp. 419-435.